Randomisierte Algorithmen

Eine Zusammenfassung von randomisierten Algorithmen, in Form eines Blogposts.

Target-Shooting

$S$ := Covid-Geimpfte Bevölkerung

$U$ := Schweizer Bevölkerung

Welcher Prozentsatz der Schweizer Bevölkerung ist geimpft?

=> eine Approximation für $|S| / |U|$ gesucht

Idee: $N$ Elemente $u_1,\cdots,u_N$ aus U auswählen und dann den daraus den Anteil der Elemente aus $S$ bestimmen. Dafür müssen die $N$ Elemente aus $U$ zufällig, gleichverteilt und unabhängig gewählt sein.

Wie man $N$ wählen muss, um eine Erfolgs-/Fehlerwahrscheinlichkeit zu erreichen, steht in der Formelsammlung. Wir stellen in der Formel für $N$ fest, die Fehlerwahrscheinlichkeit $\delta$ geht nur logarithmisch ein.

$\delta$ := gewünschte maximale Fehlerwahrscheinlichkeit

$\epsilon$ := maximal akzeptable Abweichung damit mit Wahrscheinlichkeit 1-$\delta$ die Approximation innerhalb der Abweichung liegt

Duplikate finden

Gegeben sei ein Datensatz $S$ mit $n$ Elementen. Nun müssen wir alle Duplikate (identische Elemente) in diesem Datensatz finden.

1. Ansatz: Sortiere die Elemente und durchlaufe die sortierte Folge, nur aufeinanderfolgende Elemente können potentiell Duplikate voneinander sein. Dies kostet $O(n \log n)$ für das Sortieren und $O(n + |C|)$ für das anschliessende durchlaufen.

Da Speicherzugriffe sowie Vergleiche als sehr teuer anzunehmen sind, da Elemente aus $S$ gross sind, suchen wir einen sparsameren Ansatz.

2. Ansatz: Wir verwenden eine Hashfunktion welche effizient berechenbar ist und sich zufällig verhält. Wir bilden eine grössere Eingabemenge (wovon $S$ eine Teilmenge ist), auf eine kleinere Zielmenge, die Hashwerte, ab. Die Hashwerte sollen zufällig gleichverteilt auftreten, und es gilt

Um Duplikate zu finden, hashen wir nun zuerst den Datensatz, dann sortieren wir nach Hashwert, durchlaufen anschliessend die sortierten Hashwerte um Duplikate zu finden und für Kollisionen zu prüfen. Das alles ist viel günstiger, denn die Zielmenge der Hashfunktion ist viel kleiner als die Eingabemenge, also sparen wir uns die teueren Speicherzugriffe sowie Vergleiche, welche im 1. Ansatz ein Problem darstellten.

Kollisionen sind Elemente welchen den gleichen Hashwert zugeschrieben werden, welche aber keine Duplikate voneinander sind. Sei $m$ die Anzahl der Hashwerte die möglich sind. Was ist die W’keit das zwei beliebige Elemente eine Kollision darstellen?

Da wir $\binom{n}{2}$ Paare von Elementen aus $S$ ziehen können, und tatsächliche Duplikate nicht als Kollisionen zählen, können wir eine obere Schranke für die Anzahl Kollisionen wie folgt abschätzen (wenn es keine Duplikate gibt dann gilt sogar $=$ anstatt $\leq$)

Laufzeit: $O(n)$ für die Hashmap + $O(n \log n)$ für das Sortieren von + $O(n + |C|)$ für das Durchlaufen, sowie $O(n \log n)$ Speicher ($O(n \log n)$ für die Indizes und $O(n \log m)$ für die Hashwerte)

Bloom Filter: $k$ Hashfunktionen kombiniert in ein Hash-Tuple, Sammeln von Wiederholungen in einer Liste $L$

Ergebnis "keine Duplikate" immer korrekt, Ergebnis "Duplikat gefunden" nicht immer korrekt

Primzahltest

Gesucht: Ist die Zahl $n$ prim?

Euklidisch

$a$ := Zufallszahl zwischen $2$ und $n-1$

$ggt(a,n)>1 \iff \text{nicht Prim}$

Ausgabe "nicht Prim" immer korrekt, Ausgabe "Prim" falsch mit Wahrscheinlichkeit $\frac{|Z_n^*|}{n-1}$

Fermat

$a$ := Zufallszahl zwischen $2$ und $n-1$

Ausgabe "nicht Prim" immer korrekt, Ausgabe "Prim" falsch mit Wahrscheinlichkeit $<\frac{1}{2}$ ausser wenn n eine Carmichael Zahl ist

Charmichael Zahl: $n$ ist nicht prim und für alle a gibt der Fermattest fälschlicherweise Prim aus

Miller Rabin

$a$ := Zufallszahl zwischen $2$ und $n-1$

Wenn gilt:

1. $a^{n-1}=1$
2. $a^{\frac{n-1}{2}} = 1 \text{ oder } n-1$
3. exponent durch $2$ teilen bis $\frac{n-1}{2^i}$ ungerade oder es nicht $1$ oder $n-1$ ist

Ausgabe "nicht Prim" immer korrekt, Ausgabe "Prim" falsch mit Wahrscheinlichkeit $<\frac{1}{4}$

Randomisiertes Quicksort

Indem wir unser Pivotelement zufällig wählen, können wir verhindern dass bestimmte Inputs ein worst-case Szenario ergeben. Wir interessieren uns für die erwartete Laufzeit, und hoffen diese für alle Eingaben möglichst zu verringern.

Wenn das Anfangs-Zahlenarray zufällig angeordnet ist, dann hat ein standardmässiges Quicksort genauso viele erwartete Vergleiche wie das randomisierte Quicksort. Merke: wenn Elemente nicht alle einzigartig sind, dann stimmt die Schranke nicht mehr (wegen Abhängigkeit von Zufallsvariablen)

Quickselect

Random Pivot wählen und so ein Element suchen.

Suchbaum

Randomisiertes Quicksort baut implizit einen zufälligen Suchbaum auf, wobei das erste Pivot die Wurzel des Baums ist, das linke Kind der Wurzel ist das Pivot der linken Teilhälfte, usw.

Die tiefe eines Elements im Baum ist dabei gleich der Anzahl Vergleiche mit dem Element als Nichtpivot im Quicksort.

Lange Pfade

Enthält ein Graph einen Pfad der Länge $l$? Ein Pfad der Länge $l$ hat $l$ Kanten und $l+1$ Knoten.

Dieses Problem ist NP-Vollständig (vermutlich).

Wenn $l$ klein ist, genauer gesagt $B \in O(\log n)$, dann können wir das Problem in polynomieller Zeit mit DP lösen. Dazu führen wir das Bunte Pfade Problem ein.

Bunte Pfade

Sei $k$ eine natürliche Zahl. Sei $G$ ein Graph mit einer nicht notwendigerweise gültige Färbung $\gamma:V\rightarrow[k]$

Gibt es einen bunten Pfad der Länge $k-1$ (d.h. mit K Knoten)? $\iff$ Gib es einen Pfad der Länge $k-1$ wobei alle Knoten im Pfad paarweise verschiedene Farben haben? Wir definieren

Bemerke, dass ein bunter Pfad der Länge $i$ zu $v$ aus einem $\gamma(V)$-freien bunten Pfad der Länge $i-1$ zu einem Nachbarn $x$ von $v$ plus der Kante zu $v$ besteht. So können wir mithilfe von $i-1$ langen bunten Pfaden, bunte Pfade der Länge $i$ konstruieren. Wenn wir mit allen möglichen Pfaden der Länge $0$ anfangen ($n$ viele), dann können wir für jeden solchen Pfad alle Pfade konstruieren die um $1$ länger sind, und somit aufbauend alle Pfade der Länge $0,1,\dots,i-1,i$ konstruieren.

Kehren wir nun zu unserem ursprünglichen Problem zurück. Um herauszufinden ob unser Graph einen Pfad der Länge $l$ enthält, färben wir unseren Graph zufällig mit $l+1$ Farben, und suchen nach einem bunten Pfad der Länge $l$ (mit $l+1$ Knoten). Wenn G einen solchen bunten Pfad mit $l+1$ Knoten enthält, dann ist die Wahrscheinlichkeit das unser Algorithmus, mit einer zufälligen Färbung, einen solchen findet, $\geq \text{Pr[P ist bunt]} = (l+1)!/(l+1)^{l+1}\geq e^{-(l+1)}$. Somit beträgt die erwartete Anzahl Versuche bis man einen solchen bunten Pfad findet $\leq e^{l+1}$, wegen der Geometrischen Verteilung mit Parameter $e^{-(l+1)}$.

Laufzeit

Ein Versuch dauert $O(2^{l+1}(l+1)m) \in O(2^llm)$ , und damit wir eine Fehlerwahrscheinlichkeit von $\leq e^{-\lambda}$ haben, wiederholen wir den Algorithmus $\lceil \lambda e^{(l+1)}\rceil$ Mal.

Der bunte Pfade Algorithmus an sich läuft für $k \in O(\log n)$ in polynomialer Laufzeit, genauer gesagt für $k = \log n$ in $O(mn\log n)$.

DAGs

Alle Kanten mit $-1$ gewichten und dann den kürzesten Pfad berechnen mit Bellman-Ford. Das Resultat ist der längste Pfad.

Mincut

$\mu(G) :=$ Kardinalität eines kleinstmöglichen Kantenschnitts in $G$

In einer Kantenkontraktion einer Kante verschmelzen wir die beiden inzidenten Knoten zu einem Knoten.

Es gilt: $\mu(G/e) \geq \mu(G)$, bzw. Im Allgemeinen kann $\mu$ durch Kontraktion nie fallen, und $\mu$ bleibt gleich falls es einen minimalen Schnitt ohne $e$ gibt. Wir wollen $\mu$ herausfinden, also wollen wir die Kanten kontrahieren, welche nicht in einem minimalen Schnitt sind.

Falls es einen minimalen Schnitt $C$ gibt, aus dem nie eine Kante kontrahiert wird (per Zufall), so gibt der folgende Algorithmus tatsächlich $\mu(G)$ aus

1
während der Graph mehr als 2 Knoten hat:
2
  kontrahiere eine zufällige Kante
3
return Grösse des eindeutigen Schnitts

Die Idee ist nun, den Zufallsalgorithmus so oft zu wiederholen, sodass er mit einer hohen Wahrscheinlichkeit tatsächlich $\mu(G)$ ausgibt. Sei die Wahrscheinlichkeit das der Algorithmus $\mu(G)$ ausgibt $\hat p(n)$

Somit müssen wir erwartet höchstens $\binom{n}{2}$ Mal den Algorithmus wiederholen bis wir das erste Mal $\mu(G)$ ausgeben.

Laufzeit

Für $\lambda \binom{n}{2}$-malige Wiederholung hat der ganze Algorithmus eine Laufzeit von $O(\lambda n^4)$ und die Erfolgswahrscheinlichkeit ist $1-e^{-\lambda}$ resp. die Fehlerwahrscheinlichkeit ist $e^{-\lambda}$. Somit haben wir mit $\lambda = \ln n$ einen $O(n^4 \log n)$ Algorithmus mit Fehlerwahrscheinlichkeit $\leq \frac{1}{n}$

Bootstrapping

Mit bootstrapping können wir unseren randomisieren Algorithmus um ein Vielfaches verbessern. Merke das in den letzten paar Schritten die Wahrscheinlichkeit eine im mincut enthaltene Kante zu kontrahieren, und somit ein zu hohes/fehlerhaftes Resultat zurückzugeben, sehr hoch ist. Im Allgemeinen steigt die Wahrscheinlichkeit eine "falsche" Kante zu kontrahieren mit jeder "korrekt" kontrahierten Kante an, somit haben wir in den letzten Schritten eine immens hohe Fehlerwahrscheinlichkeit.

Um dies zu umgehen wenden wir unseren langsamen, deterministischen Algorithmus genau für die wenigen letzten Schritte an, wo unsere Fehlerwahrscheinlichkeit so gross ist. Das kann man als Strategiewechsel im kritischen Bereich bezeichnen. Wann genau dieser Strategiewechsel am besten eintreten soll, um insgesamte Laufzeit und Erfolgswahrscheinlichkeit zu optimieren, kann kalibriert werden. Mit $t = \sqrt{n}$ ist der Algorithmus statt $O(\lambda n^4)$ nur noch $O(\lambda n^3)$. Dies ist eine 1-fache Anwendung von Bootstrapping. Nun bietet es sich an, auf diesen verschnellerten Algorithmus noch einmal Bootstrapping anzuwenden. Im "Limit", sprich mit "unendlich" wiederholtem bootstrapping, haben wir einen $O(n^2 \text{polylog}(n))$-Algorithmus, mit der gleichen Erfolgswahrscheinlichkeit wie der ursprüngliche Algorithmus.

Kleinster umschliessender Kreis

Gegeben eine engliche Punktemenge, finden wir den Kreis mit kleinstem Radius, der die Punktemenge umschliesst. Dieser Kreis $C(P)$ für eine beliebige Punktemenge $P$ ist immer eindeutig, sprich es gibt keine Punktemenge wofür es zwei unterschiedliche kleinste umschliessende Kreise gibt. Auch ist bekannt, das dieser kleinste umschliessende Kreis von drei "äussersten" Punkten eindeutig definiert wird. Somit haben wir unseren deterministischen Algorithmus

x
1
Iteriere durch alle möglichen 3-Tupel von Punkten
2
  C(Q) <- Bilde den kleinsten umschliessenden Kreis von diesen 3 Punkten
3
  wenn C(Q) alle Punkte umschliesst:
4
    return C(Q) ist der kleinste umschliessende Kreis der Punktemenge

Dieser Algorithmus läuft in $O(n^4)$. Wir können ihn verbessern, indem wir mit dem Radius arbeiten und so auf eine schlauere Weise die if-Bedingung $O(1)$ statt $O(n)$ kostet $\implies O(n^3)$ Algorithmus.

Nun wollen wir einen randomisierten Las-Vegas Algorithmus betrachten, welcher auch das korrekte Ergebnis ausgibt und im Erwartungswert schneller läuft. Dazu wählen wir 3 Punkte zufällig - und falls dies nicht der kleinste umschliessende Kreis ist - geben wir den Punkten ausserhalb dieses Kreises eine höhere Chance gewählt zu werden, indem wir die Punktemenge ausserhalb des Kreises verdoppeln. Je öfter wir zufällig 3 Punkte ziehen, desto eher werden wir Punkte wählen, welche weit aussen sind, bzw. je weiter aussen ein Punkt ist, desto öfter soll dieser tendenziell gewählt werden. Dies ist recht effektiv, denn die "äussersten" 3 Punkte spannen den kleinsten umschliessenden Kreis - wobei "äusserst" natürlich etwas arbiträr ist.

Analyse

Wir können jede Runde dieses randomisierten Algorithmus in $O(n)$ Zeit implementieren. Die genaue Analyse für die Anzahl Runden ist kompliziert und kann auf den Slides (Lecture 23) angeschaut werden, doch wir haben $O(\log n)$ Wiederholungen (im Erwartungswert) und somit da jede Wiederholung/Runde $O(n)$ kostet, hat der randomisierte Algorithmus eine erwartete Laufzeit von $O(n \log n)$.

Höhrere Dimensionen

In $d$ Dimensionen braucht es $d+1$ Punkte, um einen Kreis/Kugel/... in der respektiven Dimension eindeutig definieren zu können. Somit lässt sich dieser Algorithmus auch auf weitere Dimensionen erweitern.

Konvexe Hülle

Ist zwar kein randomisierter Algorithmus, aber dafür noch interessant

Eine konvexe Hülle einer Punktemenge $S$, bezeichnet als $conv(S)$, ist der Schnitt aller konvexen Mengen, die $S$ enthalten. In verständlichen Worten: eine konvexe Hülle sind Liniensegmente welche eine Punktemenge umranden, und zwar so, dass das resultierende Polygon konvex und kleinstmöglich ist. Die Ecken des Polygons sind Punkte der Menge, und das Polygon "umrandet" alle Punkte der Menge.

Wir gehen davon aus, keine 3 Punkte liegen auf einer Geraden und alle Punkte haben verschiedene $x$-Koordinaten.

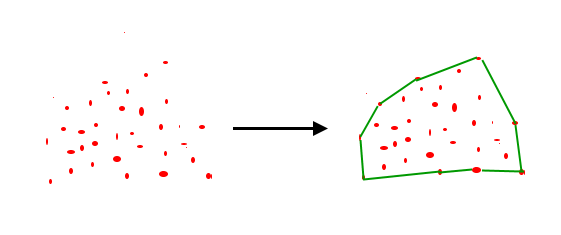
Jarvis Wrap

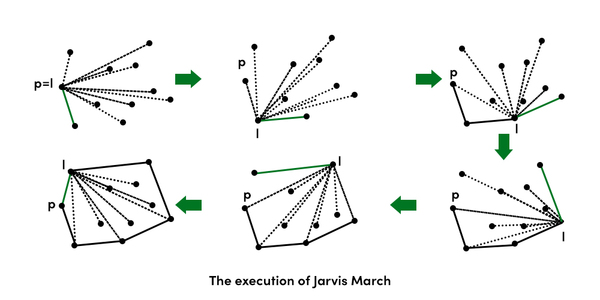
Wir fangen an mit dem Punkt $u$ mit der kleinsten $x$-Koordinate, und suchen einen Punkt $v$, sodass alle anderen Punkte links von der Geraden zwischen $u$ und $v$ liegen. Wegen unseren vereinfachenden Annahmen, gibt es einen solchen Punkt immer. Solch ein Schritt des Jarvis Wrap kostet $O(n)$, denn wir iterieren durch $O(n)$ viele Punkte, bis wir einen finden, wozu die Gerade zwischen $u$ und $v$ eine Randkante ist. Wie die Relation "ist links von" ermittelt wird, hat etwas mit LinAlg und Determinanten zu tun - ptsd. Wir müssen unseren Jarvis-Wrap Schritt genauso oft ausführen, wie es Kanten in der konvexen Hülle gibt, denn pro Schritt finden wir genau eine neue Kante der Hülle. Somit haben wir die Laufzeit $O(nh)$

LocalRepair

Wir sortieren die Punktemenge $P=(p_1,\dots,p_n)$ aufsteigend nach x-Koordinate. Nun verdoppeln wir das Polygon und fügen die verdoppelten Kanten invertiert in die Polygonmenge $\implies P = (p_1,\dots,p_n,p_{n-1},\dots,p_2)$. Nun konvexifizieren wir dieses Polygon

Wir entfernen einen Punkt $q_i$ falls er links von der Geraden $q_{i-1}q_{i+1}$ liegt. Führen wir dies aus, so konvexifizieren wir das Polygon und erhalten am Schluss die konvexe Hülle sowie eine Triangulierung der Punkte, dessen Umriss die konvexe Hülle ergibt.

Der Algorithmus läuft in $O(n \log n)$, wobei das Sortieren $O(n\log n)$ kostet und das konvexifizieren bloss $O(n)$. Also wenn die Punkte bereits in sortierter Reihenfolge gegeben sind, dann braucht LocalRepair $O(n)$ Zeit.

Konvexe Mengen

~Tobi